三类方程的基本解
基本解只与方程相关, 与边界条件无关. 以下将考虑 Laplace 方程, 热方程和波动方程的基本解.
方程 \(L\) 基本解的定义为右端项为 delta 函数的响应: \[ L[u] = \delta \]
Laplace 方程的基本解
先给出结论: 设 Laplace 方程的基本解为 \(N(x)\) \[
-\Delta N = \delta
\] 那么对不同的维度, 解 \(N(x)\)
为 \[
\boxed{N(x) = \left\{\begin{array}{cl}
\dfrac{1}{(d-2) S_d} |x|^{2-d}, &d \neq 2\\
- \dfrac{1}{2\pi} \ln|x|, \quad & d = 2
\end{array}\right.}
\] 式中, \(S_d\) 为 \(d\) 维单位球的表面积. 分别列出一维,
二维和三维情景下 Laplace 方程的基本解: \[
\boxed{N(x) = \left\{\begin{array}{cl}
-\dfrac{1}{2} |x|, & d = 1\\
-\dfrac{1}{2\pi} \ln|x|, & d = 2\\
\dfrac{1}{4\pi} \dfrac{1}{|x|}, & d =3
\end{array}\right.}
\]

接下来, 我们会用两种方式推导基本解. 第一种方式是利用 Laplace 解的径向对称性, 因此假设方程的解 \(u(x)\) 可以写成关于距原点距离为 \(r\) 的函数 \(v(r)\): \[ u(x) = v(r), \quad r = |x| \] 将径向对称解代入到 Laplace 方程中的二阶导数项 \[ \frac{\partial v(|x|)}{\partial x_i} = v' \frac{x_i}{|x|}, \quad \frac{\partial^2 v(|x|)}{\partial x_i^2} = v'' \frac{x_i^2}{|x|^2} + v' \frac{|x|^2 - x_i^2}{|x|^{3}} \] 求和得到关于 \(r\) 的常微分方程 \[ \Delta u = v'' + \frac{(d-1)}{r}v' = 0 \] 当 \(d \neq 1\) 时, 上述微分方程的一个不平凡解为 \[ v' = Ar^{1-d}, \quad v = \begin{cases} A \ln r, &d = 2 \\ B r^{2-d}, &d > 2 \end{cases} \] 这样, 除了待定常数之外,Laplace 方程基本解的形式是已经确定的了.
另一种, 也是更常规的方法, 是使用 Fourier 变换. 方程两端作 Fourier 变换得到 \[ 4 \pi^2 |\xi|^2 \widehat N = 1, \quad |\xi|^2 \triangleq \xi_i \xi_i \] 所以方程的基本解可以通过 Fourier 逆变换表示为 \[ N(x) = \mathscr{F}^{-1}[\widehat N] = \int_{\mathbb{R}^d} \frac{1}{4\pi^2 |\xi|^2} e^{i2\pi\xi \cdot x} ~\mathrm{d}\xi \] 注意到 \(\widehat{N}\) 是 \(\alpha=-2\) 的齐次径向对称函数, 所以 \(N\) 是 \(-d-\alpha = -d+2\) 齐次径向对称函数, 因此 \(N\) 可以写成 \[ N(x) = N(|x|\frac{x}{|x|}) = |x|^{2-d} N_{0}(1) \] 为确定常数 \(N_0(1)\), 对 \(\Delta N\) 在球 \(B_{\varepsilon}(0)\) 上积分, 并应用 Gauss 公式, 得到 \[ \int_{B_{\varepsilon}} -\Delta N ~\mathrm{d}x = 1 = - \int_{\partial B_{\varepsilon}} n \cdot \nabla N ~\mathrm{d} \sigma(x) \] 径向对称函数的法向导数为 \[ \boxed{\nabla N = N_0'(r)\frac{x_i}{|x|} = N_0'(r) n, \quad n \cdot \nabla N = N_{0}'(r)} \] 所以 \[ 1 = - \int_{\partial B_{\varepsilon}} N_{0}' ~\mathrm{d} \sigma(x) = - N_{0}'(\varepsilon) S_{d} \varepsilon^{d-1} = (d-2) S_{d} N_0(1) \] 由此得到 \[ N(x) = \frac{1}{(d-2) S_{d}} |x|^{2-d} \]
[!Important]
式中对于 \(d=2\) 的情景是不适用的, 不过可以考虑这样 (虽然不令人很信服) 的极限: \(d = 2 + \varepsilon\), 那么, \[ N(x) = \frac{1}{\omega_{1+ \varepsilon} \varepsilon }|x|^{-\varepsilon} = \frac{1}{2\pi} ~ \frac{1}{ \varepsilon }|x|^{-\varepsilon} \] 将上式右端项关于 \(\varepsilon\) 渐进展开得到 \[ \frac{1}{ \varepsilon }|x|^{-\varepsilon} = \frac{1}{ \varepsilon }e^{-\varepsilon\ln|x|} \sim \frac{1}{\varepsilon} ( 1 - \boxed{\varepsilon \ln |x|} + o(\varepsilon) ) \] 最后得到 \[ N(x) = -\frac{1}{2\pi} \ln|x| \]
[!NOTE]
\(d=1\) 时的基本解
此时方程为 \[ -u'' = \delta \] 该方程在 \(x=0\) 处有奇性, 所以分别对 \(x>0\) 和 \(x<0\) 区域分别求解得到 \[ u = \begin{cases} c_1 x, & x<0\\ c_2 x, & x>0 \end{cases} \] 基本解中忽略常数项. 为确定积分中出现的常数, 还需要利用如下性质. 首先是对称性, 这要求 \(c_1 = -c_2 = c\). 然后对方程在区间 \((-\varepsilon,\varepsilon)\) 上积分得到 \[ -\int_{-\varepsilon}^{\varepsilon} u'' ~\mathrm{d}x = 1 \] 分别对 \((0,\varepsilon)\) 和 \((-\varepsilon,0)\) 两个区间段积分得到 \[ -u'|_{0^+}^{\varepsilon} - u'|_{-\varepsilon}^{0^-} = -c + u'(0^+)-u'(0^-)-c = [u'(0)] - 2c = 1 \] 如果设置间断条件 \([u'(0)] = 0\), 那么 \[ c = -\frac{1}{2} \]
热方程的基本解
热方程基本解满足的方程和初始条件为 \[
\left\{\begin{array}{c}
\dfrac{\partial H}{\partial t} = \Delta H \\
H(x,0) = \delta(x)
\end{array}\right.
\] 应用 Fourier 变换, 得到 \[
\left\{\begin{array}{c}
\dfrac{\mathrm{d} \widehat H}{\mathrm{d} t} + 4 \pi^2 |\xi|^2 \widehat H
\\
\widehat H(0) = 1
\end{array}\right.
\] 求解上述微分方程, 得到 \[
\widehat H(t) = e^{-4\pi^2 |\xi|^2 t}
\] 所以热方程的基本解为 \[
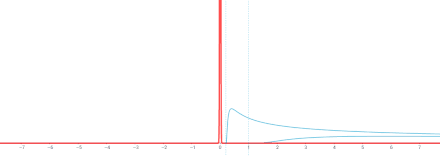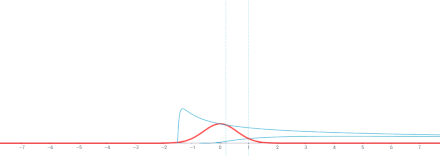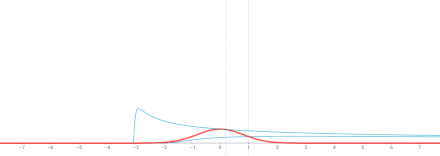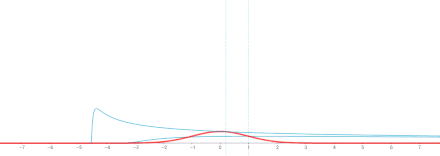
\boxed{H(x,t) = \frac{1}{(4\pi t)^{d/2}} e^{- |x|^2/4t}}
\] 
另一种得到热方程基本解的方式是自相似方法. 如果 \(H(x,t)\) 满足热方程和初始条件, 那么, \(cH(\lambda x, \lambda^2 t)\) 同样也满足热方程. 为保证初始条件一致, \(cH(\lambda x, 0) = c\delta(\lambda x)\) 应等于 \(\delta(x)\), 这要求 \(c = \lambda^d\). 所以, 对任意 \(\lambda \neq 0\), \[ H(x,t) = \lambda^d H(\lambda x, \lambda^2 t) \] 如果取 \(\lambda = 1/\sqrt{t}\), 那么 \[ H(x,t) = t^{-d/2} H(x/\sqrt{t}, 1) \] 再考虑到热方程关于空间的微分是径向对称的, 所以 \(H(x/\sqrt{t}, 1)\) 可以表示为 \(\mathbb{R}\) 上单变量的函数 \(v(r)\), \(r = |x|/\sqrt{t}\): \[ H(x,t) = t^{-d/2} v(r) \] 将解代入到热方程 \(\partial_t H = \Delta H\) 中得到 \[ -\frac{d}{2} t^{-d/2 - 1} v + t^{-d/2} v' \frac{\mathrm{d} r}{\mathrm{d} t} = t^{-d/2} (v''/t + \frac{d-1}{|x|}v'/\sqrt{t}) \] 这就得到微分方程 \[ v'' + \left(\frac{d-1}{r} + \frac{1}{2} r \right)v' + \frac{d}{2} v = 0 \] 也即 \[ (r^{d-1} v')' + \frac{1}{2} (r^d v)' = 0 \Rightarrow r^{d-1} v' + \frac{1}{2} r^d v = \mathrm{const} \] 令常数等于 0, 那么 \[ v = c e^{-r^2/4} \]
波动方程的基本解
在波动方程基本解的定义当中, 函数 \(\delta\) 放在了初始速度项: \[ \frac{\partial^2 W}{\partial t^2} - \Delta W = 0,\\ W(x, 0) = 0, \\ \partial_t W(x,0) = \delta \]