p-范数下的圆周率

发表于 更新于 阅读次数：

待求解积分的解析性质

在 \(p\)-范数下的圆周率定义为 \[ \pi_p \triangleq \frac{2}{p} \int_{0}^{1} \left( u^{1-p} + (1-u)^{1-p} \right)^{1/p} ~\mathrm{d}u, \quad 1 < p \leq \infty \tag{1} \] 圆周率 \(\pi_p\) 具有如下性质

  1. \(\pi_2\) 是最小值;
  2. 如果 \({1}/{p} + {1}/{q} = 1\), 那么 \(\pi_p = \pi_q\).

证明的参考文献为

  1. Adler, C. L., & Tanton, J. (2000). π is the Minimum Value for Pi. The College Mathematics Journal, 31(2), 102–106.
  2. πp, the value of π in lp - Stanford Mathematics

对不同的 \(p\) 取值, 积分项函数的图像为

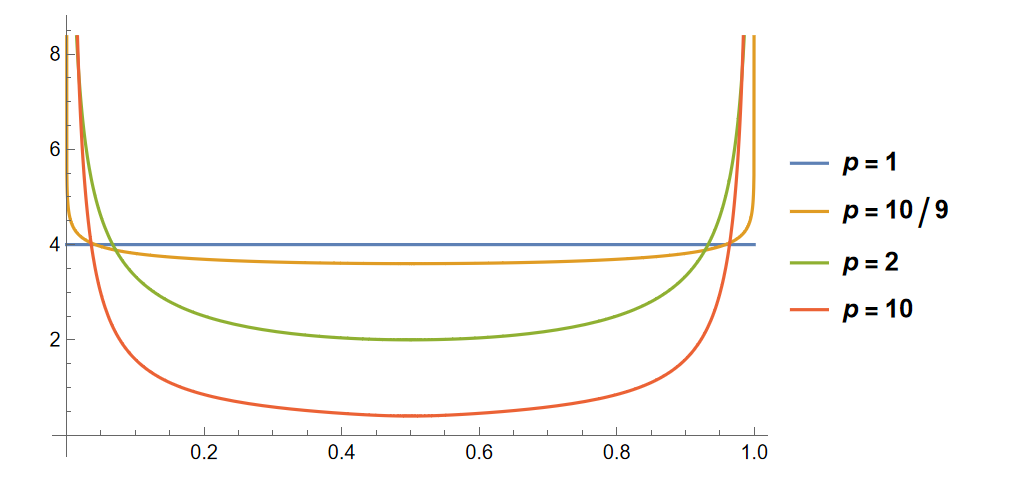
image-20240603131849757

由此可以看到积分项函数的性质为

  • 在 \(x=0\) 和 \(x=1\) 处出现爆破, 因此使用的数值方法必须考虑到这一情况；
  • 关于 \(x=0.5\) 对称, 因此可以只考虑区间 \((0,0.5)\) 上的积分

数值积分需要考虑的问题

根据对称性, 式 (1) 可以转换到区间 \((0,0.5)\) 上的积分: \[ \pi_p = \frac{4}{p} \int_{0}^{0.5} \left( u^{1-p} + (1-u)^{1-p} \right)^{1/p} ~\mathrm{d}u \] 定义被积函数 \(f(x)\) 为 \[ f(x) \triangleq \frac{4}{p}\left( x^{1-p} + (1-x)^{1-p} \right)^{1/p} \] 因此 \[ \pi_p = \int_{0}^{0.5} f(u) ~\mathrm{d}u \]

如何处理瑕积分

被积函数在 \(x=0\) 处发生爆破, 在本次作业中处理该瑕点的常用且可行的方式有:

  1. 将积分区间分成 \((0,\varepsilon)\) 和 \((\varepsilon, 0.5)\), 在区间 \((0,\varepsilon)\) 上使用幂函数近似, 在区间 \((\varepsilon, 0.5)\) 使用常规的积分策略;
  2. 换元, 将积分区间 \((0,1)\) 变换到 \((0,\infty)\) 上, 同时采用的换元方式使得被积函数快速衰减, 通过延展积分区间回避掉瑕点的爆破现象.

方式 1 的一种推导思路陈述如下: 首先将 \(f(x)\) 变形为 \((1+\square)^{1/p}\) 的形式: \[ f(x) = \frac{4}{p} \frac{\left( 1 + \overbrace{(1/x-1)^{1-p}}^{\square} \right)^{1/p}}{x^{1-1/p}} \] 注意到对任意给定的 \(p\in(1,\infty)\), \[ \left( \frac{1}{x} -1 \right)^{1-p} \rightarrow 0, \quad when \quad x \rightarrow 0^+ \] 所以可以使用如下近似 \[ (1+\square)^{1/p} \sim 1 + \frac{1}{p} \square \Rightarrow f(x) \sim \underbrace{\frac{4}{p}x^{1/p-1}}_{①} + \underbrace{\frac{4}{p^2} \left( x^{1/p-1}-x^{1/p} \right)^{1-p}}_{②} \] 如果再忽略第 ② 项, 那么就可以用如下幂函数近似被积函数 \(f(x)\): \[ \widetilde f(x) = \frac{4}{p}x^{1/p-1} \] 这种忽略是合理的, 分别绘制出这两项的函数图像 (\(p=1.1\)​). 可以看到, 函数 \(f\) 在 \(x=0\) 附近的奇性完全是由第 ① 项表现出来的.

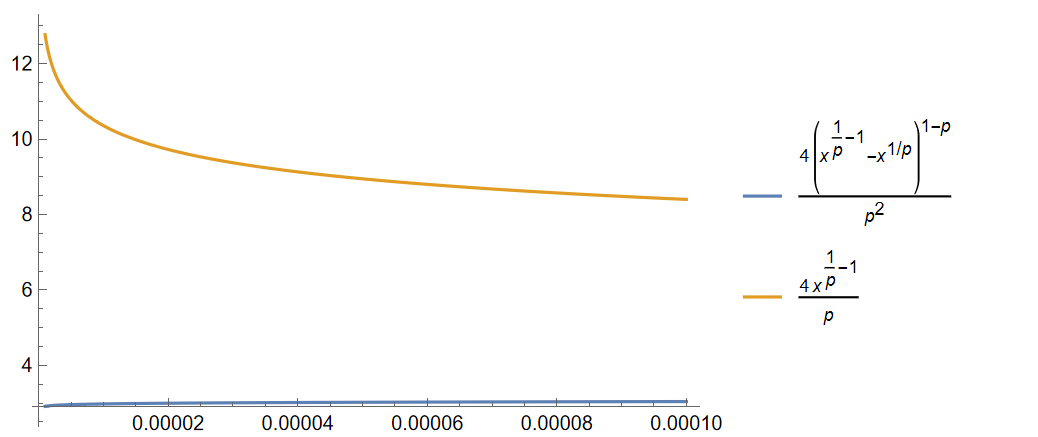
image-20240608133623497

注意到当 \(p=1\), 时, \(\widetilde f(x) \equiv 4\), \(f(x) \equiv 8\), 为了弥补这一缺陷, 可以再补充一项常数项, 最终得到的在区间 \((0,\varepsilon)\) 上的近似函数为 \[ \widetilde f(x) \triangleq \frac{4}{p}x^{1/p-1} + 4 \] 对上式在区间 \((0,\varepsilon)\) 上积分, 就得到 \[ \int_{0}^{\varepsilon} \widetilde f(x) ~\mathrm{d}x = \int_{0}^{\varepsilon} \frac{4}{p}x^{1/p-1} + 4 ~\mathrm{d}x = 4\varepsilon^{1/p} + 4\varepsilon \triangleq I_1 \] 最终 \(\pi_p\) 为 \[ \boxed{ \pi_p \approx I_1 + \int_{\varepsilon}^{0.5} f(x) ~\mathrm{d}x } \] 方式 2 中一种常用的换元方式为 Fundamentals of Numerical Computation \[ u(t) = \frac{1}{1+\exp(2\sinh t)} \] 注意到 \(t=0\) 时, \(u=0.5\); \(t\rightarrow \infty\) 时, \(x \rightarrow 0\)​. 微分关系为 \[ \mathrm{d} u = - \frac{\cosh t}{2\cosh(\sinh t)^2} ~\mathrm{d}t \] 所以 \[ \pi_p = \int_{0}^{0.5} f(u) ~\mathrm{d}u = -\int_{\infty}^{0} f(u(t)) \frac{\cosh t}{2\cosh(\sinh t)^2} ~\mathrm{d}t = \int_{0}^{\infty} f(u(t)) \frac{\cosh t}{2\cosh(\sinh t)^2} ~\mathrm{d}t \] 定义权函数 \(\omega(t)\) \[ \omega(t) \triangleq \frac{\cosh t}{2\cosh(\sinh t)^2} \] 绘制权函数的图像如下, 可以观察到, 该函数收敛很快, 当 \(t=3\) 时, \(\omega(t) = 8.0089\times10^{-8}\); 当 \(t=4\) 时, \(\omega(t) = 2.16089\times10^{-22}\). 因此在数值积分时, 可以设置初始积分区间为 \((0,3)\), 然后不断扩展积分区间. 当被积函数取值小于给定阈值之后, 停止积分, 输出结果.

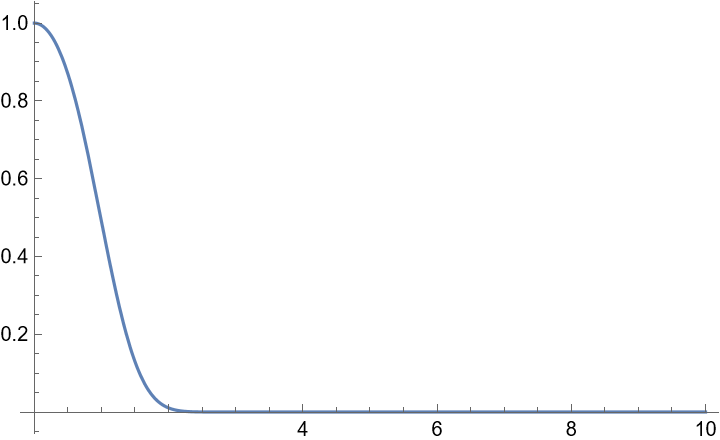
image-20240608142415330

需要指出的是, 换元方式并不是唯一的. 作业中使用到的换元方式还有 \[ u(t) = \frac{1}{1+e^{-t}} \]

如何处理 \(p\) 取较大值的情况

最方便的方式是使用最开始给出的解析性质: \[ \pi_p = \pi_q, \quad if \quad \frac{1}{p} + \frac{1}{q} = 1 \] 如果不清楚这一性质, 那么必须考虑数值计算 \(p\) 次幂可能出现的问题. 例如计算 \((0.1^{1000})^{0.001}\) 时, 正确结果为 \(0.1\), 但当 \(0.1^{1000}\) 在计算机求解时等于 \(0\), 再开 \(0.001\) 次方结果还是等于 0. 这是一些同学的程序在 \(p\) 很大时输出结果误差很大的原因.