非线性计算中的增量步与迭代方法

参考文献:

M.A.Crisfield, Non-linear Finite Element Analysis of Solids and Structures.

算例简述

本算例是希望通过一个简单的一维系统，给出非线性计算过程中增量步的概念，这是线性与非线性有限元计算之间一个很大的区别。

我们准备分析的系统如图所示

几何以及材料参数设置如下:

L = 2500; % initial truss length
z =   25; % initial offset(no stress)
E =  5e7; % Young's modulus
A =    1; % cross-section area
d = sqrt(L^2 - z^2);

系统 位移-外载 关系的解析求解

该系统外载 \(W\) 与位移 \(w\) 之间的解析关系是可以得到的，接下来我们将推导这一关系，并用它来衡量之后数值算法的准确性。

杆原长为 \(L\)，变形后杆长度 \(l\) 为： \[ l=\sqrt{(z+w)^2 +d^2 } \] 杆的变形量 \(\Delta l\) 为 \[ \Delta l \triangleq l-L=\sqrt{(z+w)^2 +d^2 }-L \] 在我们的符号约定下，\(\Delta l\) 正值表示拉伸，负值表示压缩。根据定义，杆的应变为 \[ \varepsilon \triangleq \frac{\Delta l}{L} =\frac{\sqrt{(z+w)^2 +d^2 }-L}{L} =\sqrt{ {\left( \frac{w}{L} \right)}^2 +2\left( \frac{zw}{L^2 } \right)+1 } - 1 \] 若假设 \[ L\gg z, L \gg w \tag{1} \] 那么有如下近似关系： \[ \varepsilon \approx \frac{z}{L^2}w+\frac{1}{2L^2}w^2 \]

根据受力示意图，系统内力 \(N\) 和 \(P\) 与外载 \(W\) 之间的平衡关系为： \[ W = N \sin\theta + P \tag{2} \] 又因为假设的小量关系（1），所以 \(l \approx L\)，因此 \(\sin \theta\) 可以近似表示为 \[ \sin \theta = \frac{z+w}{l} \approx \frac{z+w}{L} \tag{3} \] 杆材料的本构关系将应变 \(\varepsilon\) 与杆的内力 \(N\) 联系起来： \[ N=EA\varepsilon =EA\left( \frac{z}{L^2}w+\frac{1}{2L^2}w^2 \right) \tag{4} \] 根据弹簧的本构关系，弹簧力 \(P\) 为 \[ P=K_{\mathrm{s}} w \tag{5} \] 将式（3）（4）（5） 代入到式（2） 中，可以得到外载 \(W\) 与位移 \(w\) 的关系为 \[ W = EA\left( \frac{zw}{L^2}+\frac{1}{2}{ \left(\frac{w}{L}\right)}^2 \right) \frac{w+z}{L}+K_{ \mathrm{s} } w = \frac{EA}{L^3 }\left(z^2 w+\frac{3}{2}zw^2 +\frac{1}{2}w^3 \right)+K_{ \mathrm{s} } w \tag{6} \] 可以看到，外载与位移之间的关系是非线性的，可以用 MATLAB 作出位移-外载关系曲线的解析解：

系统 位移-外载 关系的数值求解

接下来，我们将使用 增量步 + 牛顿迭代法 来求解 位移-外载 曲线。

增量步方法

在陈述增量步方法之前，还是需要再强调一下线性问题与非线性问题之间的区别。对于线性问题，位移-外载曲线总是一条直线。因此，求解一次系统方程得到 \((w_0 ,W_0 )\)，就能够知道系统在任意外载 \(W\) 下的位移响应 \(w\)：

\[ w=\frac{w_0 }{W_0 }W \]

但在本例中，位移-外载曲线并不是直线，因此不可能像线性问题一样，让外载「一步到位」，直接得到最终的加载结果。不过，我们可以将整个加载过程分成多个增量步，在增量步足够小的时候，系统的响应是可以近似 「线性」的。

我们将加载过程分成 \(N\) 步，每一步的增量为 \(\Delta W_n\)。为了方便陈述系统在每一个加载点的状态，引入「加载时间」\(t\)，它与增量步之间的关系可以用下面的数轴来描述：

加载时间 \(t\) 并不等同于真实的物理时间。

在该增量步下，如果使用显式方法计算（\(t_{n+1}\) 时刻的未知量可全部由 \(t_{n}\) 时刻的已知量计算得到），位移增量 \(\Delta w_{n+1}\) 为 \[ \Delta w_{n+1}:={\left( \left. \frac{\mathrm{d}W}{\mathrm{d}w} \right|_{t_{n}} \right)}^{-1} \Delta W_{n+1}=K_{n}^{-1} \Delta W_{n+1} \tag{7} \]

式中，\(K_{n}\) 为外载 \(W\) 对位移 \(w\) 在 \(t_{n}\) 时刻的导数：

\[ K_{n} \triangleq \left. \frac{\mathrm{d} W}{\mathrm{d} w} \right|_{t_n} =\frac{EA}{L}{\left(\frac{z}{L}\right)}^2 +\frac{EA}{L}\left(\frac{2zw_n + w_n^2 }{L^2 }\right)+\frac{N}{L}+K_{\mathrm{s}} \]

式中，\(w_n = \sum_{k=1}^{n} \Delta w_{k}\)，\(n=0\) 时 \(w_n=0\)。对于第一次的增量步，位移 \(w_0 = 0\)，杆中的内力 \(N_0=0\)，由此计算得到点 \((0,0)\) 处的 \(K_{n}\) 为

K = 3.3500

下一步的位移增量 \(\Delta w_1\) 为

dw = -2.0896

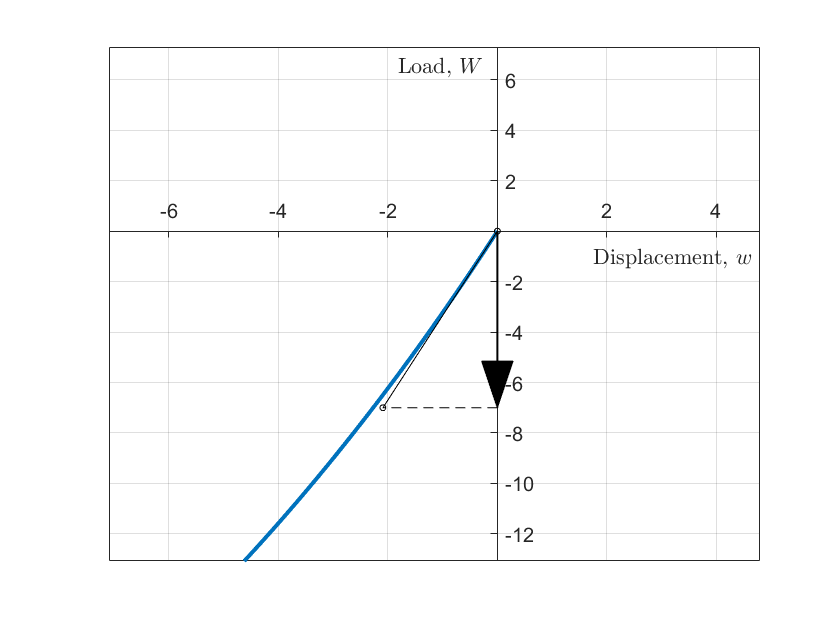
多个增量步累积计算的结果为

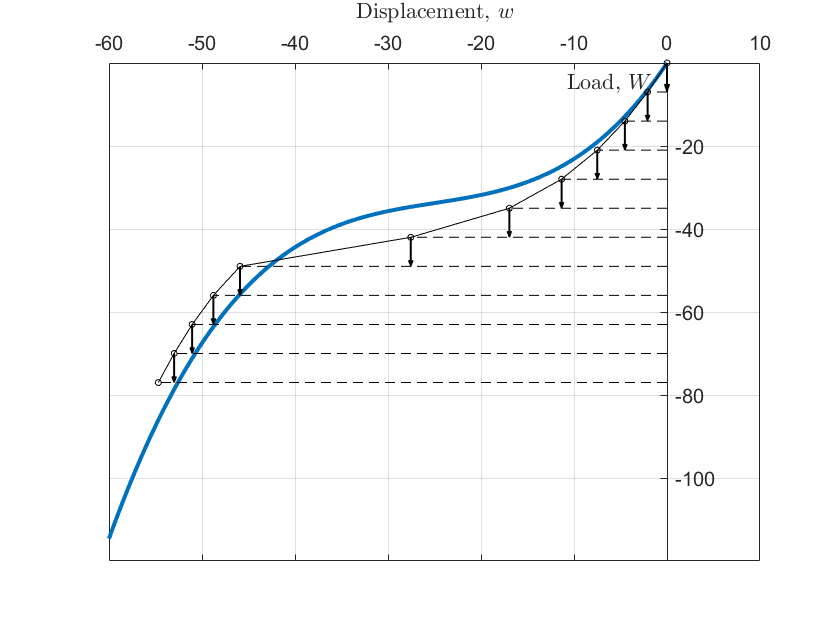
需要指出的是，只使用显式增量步方法得到的结果，系统内力与外载并不是平衡的。例如在第一个增量步时，外载增量 \(\Delta W_1 = -7\)，对应位移增量为 \(\Delta w_1\) 为

dw = -2.0896

代入式（4）中内力的计算公式，并在外载方向投影，得到杆内力与弹簧力之和为

f_ext = -6.4908

由此可见系统的内力与外载并不相等： \[ -7=f^{\mathrm{ext}} \neq f^{\mathrm{int}} = -6.4908 \]

迭代法求解

我们已经看到，如果只使用显式增量步计算，系统内外力并不是平衡的。系统内外力的差值可以定义为如下残差函数 \(g(w)\) ：

\[ g(w) \triangleq \frac{EA}{L^3 }\left(z^2 w+\frac{3}{2}zw^2 +\frac{1}{2}w^3 \right)+K_{\mathrm{s}} w-W \]

对给定的外载 \(W\)，真实位移应使得残差函数 \(g(w) \equiv 0\)。在增量步计算过程中，即使在 \(t_n\) 时刻可以保证系统内外力平衡，由于对系统在 \(\Delta W_{n+1}\) 增量步的线性假设，在 \(t_{n+1}\) 时刻的系统内外力一般并不平衡： \[ g(w_{n+1}^{(0)}) \neq 0 \] 式中，\(w_{n+1}^{(0)}\) 表示直接通过式（7）得到的结果。我们可以将 \(w_{n+1}^{(0)}\) 作为 Newton 迭代法的初值，迭代得到更好的位移增量 \(w_{n+1}^{(i+1)}\)： \[ \Delta w_{n+1}^{(i+1)} := -\left( \left. \frac{\mathrm{d}g}{\mathrm{d}w} \right|_{w_{n+1}^{(i)}} \right)^{-1} g( w_{n+1}^{(i)}), \quad w_{n+1}^{(i+1)} = w_{n+1}^{(i)} + \Delta w_{n+1}^{(i+1)} \tag{8} \]

一般形式的牛顿迭代法

我们可以将式 (8) 写成更一般的形式, 系统内力与外力在每一个增量步都应保持平衡: \[ f^{\mathrm{int}}(\sigma(\varepsilon)) - f^{\mathrm{ext}}_{i} \equiv 0, \quad i = 1,2,\ldots \] 内力通过应力得到, 应力通过本构关系与应变相关联. 定义系统第 \(i\) 步的残差函数为 \[ r_{i}(\varepsilon) \triangleq f^{\mathrm{int}}(\sigma(\varepsilon)) - f^{\mathrm{ext}}_{i}, \quad i = 1,2,\ldots \] 在第 \(n\) 个增量步时系统内外力达到平衡: \[ f^{\mathrm{int}}(\sigma(\varepsilon_n)) - f^{\mathrm{ext}}_n =0 \] 在第 \(n+1\) 个增量步时, 系统外力为 \(f^{\mathrm{ext}}_{n+1}\), 为求得使内外力平衡的 \(\varepsilon_{n+1}\), 将残差函数在 \(\varepsilon_n\) 处展开 \[ r_{n+1}(\varepsilon_n + \delta \varepsilon) \sim r_{n+1}(\varepsilon_n) + \left.\frac{\partial r_{n+1}}{\partial \varepsilon}\right|_{\varepsilon_n} \delta \varepsilon \] 并令上式等于 0, 这就得到关于 \(\delta \varepsilon\)​ 的线性方程: \[ r_{n+1}(\varepsilon_n) + \left.\frac{\partial r_{n+1}}{\partial \varepsilon}\right|_{\varepsilon_n} \delta \varepsilon = 0 \tag{$\star$} \] 在 ABAQUS 中写本构时, 程序会提供应变增量 \(\Delta \varepsilon\) (对应式 (\(\star\)) 中的 \(\varepsilon_n\)), 并要求用户返回应力增量 \(\Delta \sigma\) (用于计算 \(r_{n+1}\)) 和切线刚度模量 \(\partial \Delta \sigma / \partial \Delta \varepsilon\) (用于计算 \(\left.{\partial r_{n+1}}/{\partial \varepsilon}\right|_{\varepsilon_n}\)) 以及非线性本构要用到的状态变量. 这样 ABAQUS 内部得到 \(\delta \varepsilon\), 并进行下一步的迭代

我们可以通过如下公式衡量迭代算法的收敛速度。如果方程在前后两次迭代步的残差满足 \[ \frac{|g( w_{n+1}^{(i+1)})|}{|g( w_{n+1}^{(i)})|^M} \approx \text{Const} \] 那么该迭代算法收敛速度是 \(M\) 阶的。也就是说，每次迭代的残差与前一次迭代的 \(M\) 次方在量级上保持一致。例如在本问题中，收敛残差比值打印出的结果为

The error convergence of e_{i+1}/e_{i}^2 is 0.009203
The error convergence of e_{i+1}/e_{i}^2 is 0.030338
The error convergence of e_{i+1}/e_{i}^2 is 0.064449
The error convergence of e_{i+1}/e_{i}^2 is 0.066711
The error convergence of e_{i+1}/e_{i}^2 is 0.099625
The error convergence of e_{i+1}/e_{i}^2 is 0.099167
The error convergence of e_{i+1}/e_{i}^2 is 73.914835

所以算法（8）是平方收敛的（最后一步是因为达到了计算机浮点数精度）。这个算法的收敛速度是很快的，例如当初值残差是 E-01 量级的，而计算机浮点数精度为 E-16。那么对于平方收敛算法，只需要迭代 \[ \left( \left( \left( \left( \square^{-1} \right)^2 \right)^2 \right)^2 \right)^2 = \square^{-16} \] 4 次就可以收敛到浮点数的精度！但是，需要指出的是，算法（8）的每一次迭代过程中，都需要重新计算 \(\left( \left. \frac{\mathrm{d}g}{\mathrm{d}w} \right|_{w_{n+1}^{(i)}} \right)^{-1}\)​，所以才能达到 平方阶的收敛速度。在本算例中可能无法体现出计算切线刚度矩阵的难度（本例切线刚度矩阵为标量），但对于更复杂的非线性系统，计算切线刚度矩阵是非常消耗时间的。

不过，保证收敛的迭代算法并不是唯一的。我们可以放松对收敛速度的要求，降低计算切线刚度矩阵的难度。一种方法是，在计算得到第一次迭代时计算得到的切线刚度矩阵后，将它作为后续迭代中刚度矩阵的近似： \[ \Delta w_{n+1}^{(i+1)} = -\left( \left. \frac{\mathrm{d}g}{\mathrm{d}w} \right|_{ w_{n+1}^\textcolor{red}{(0)} } \right)^{-1} g( w_{n+1}^{(i)}), \quad w_{n+1}^{(i+1)} = w_{n+1}^{(i)} + \Delta w_{n+1}^{(i+1)} \tag{9} \] 算法（9）的收敛速度没有算法（8）速度那么快。例如算例在使用算法（9）时的一个加载步的迭代过程为：

Current load step: 1 
Current iteration step: 1; The out of balance force is 9.5086E-02
Current iteration step: 2; The out of balance force is 6.0843E-03
Current iteration step: 3; The out of balance force is 3.9566E-04
Current iteration step: 4; The out of balance force is 2.5756E-05
Current iteration step: 5; The out of balance force is 1.6768E-06
Current iteration step: 6; The out of balance force is 1.0916E-07
Current iteration step: 7; The out of balance force is 7.1064E-09
Current iteration step: 8; The out of balance force is 4.6264E-10
Current iteration step: 9; The out of balance force is 3.0118E-11
Current iteration step: 10; The out of balance force is 1.9611E-12
Current iteration step: 11; The out of balance force is 1.2745E-13

算法（8）和（9）在每一个加载步的迭代过程可以用下图清晰地表示出来：

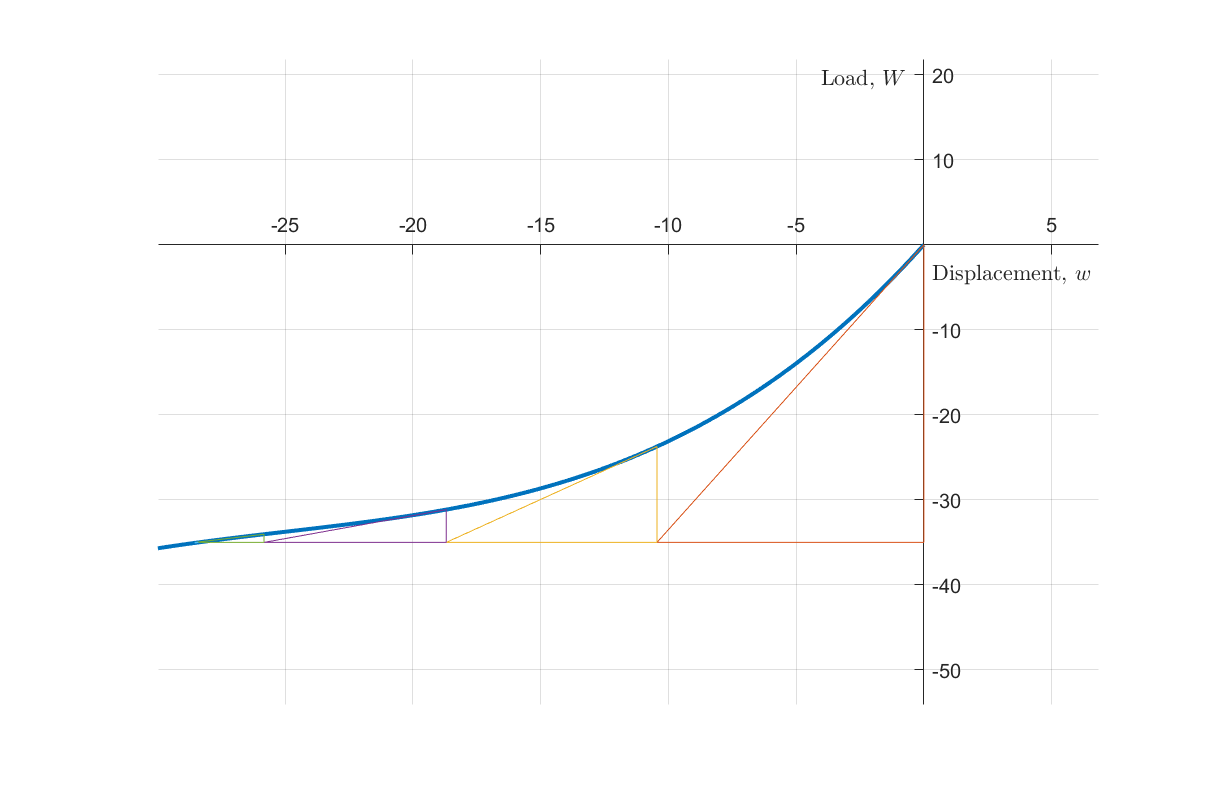
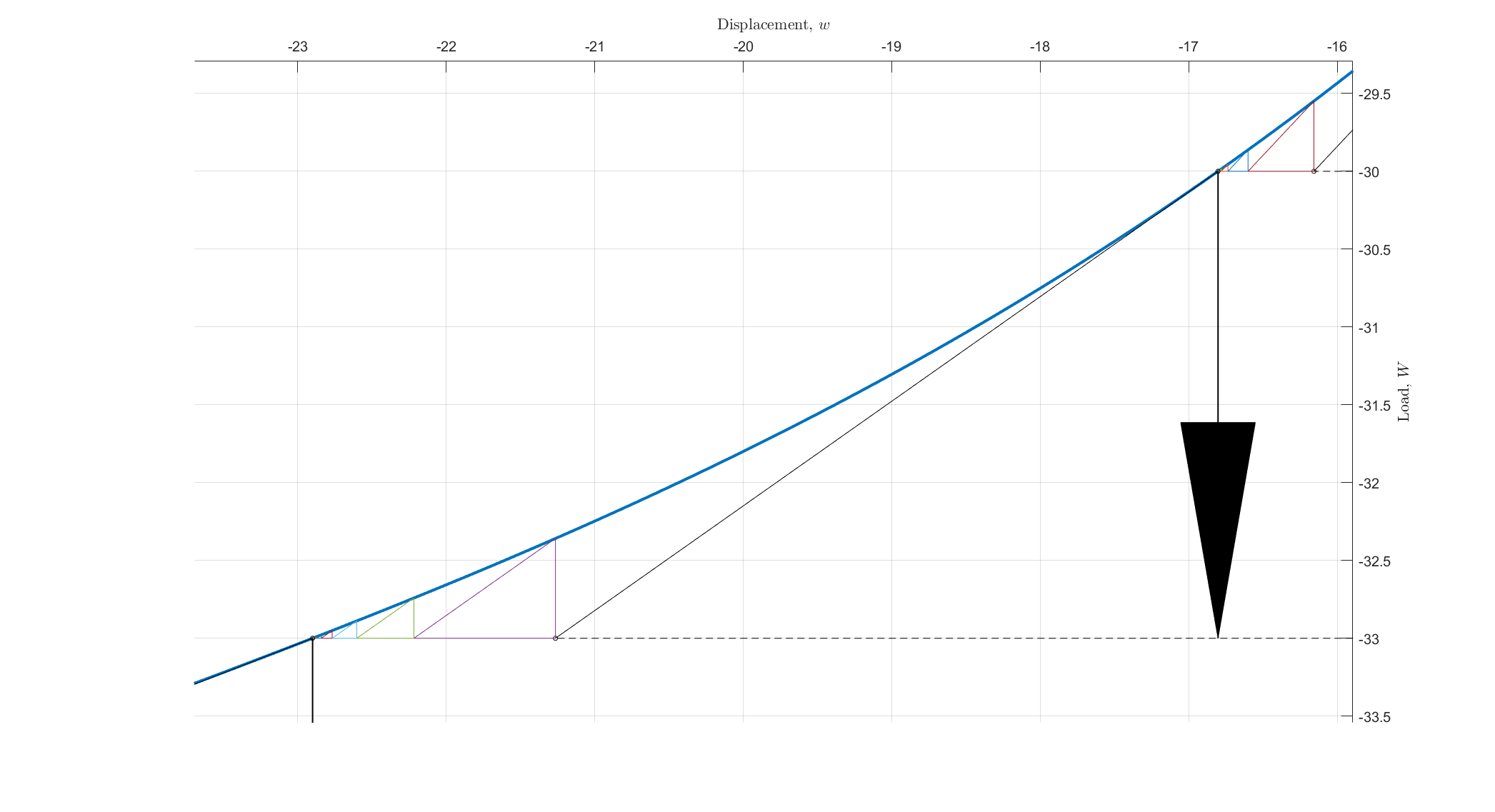
切线刚度矩阵可以使用近似值，这会影响迭代收敛的速度，但一般不会影响迭代收敛到准确值的精度。但是，残差 \(g( w_{n+1}^{(i)})\) 的计算结果必须是准确的。如果系统的内力与外力计算误差太大，那么无论怎样提高切线刚度矩阵的精度，或者增加迭代的次数，或者减小增量步的步长，都不会得到正确的计算结果！

最终，我们给出在使用增量步，并对每一个增量步的结果进行 Newton 迭代，使得内力等于外载后得到的数值计算结果：

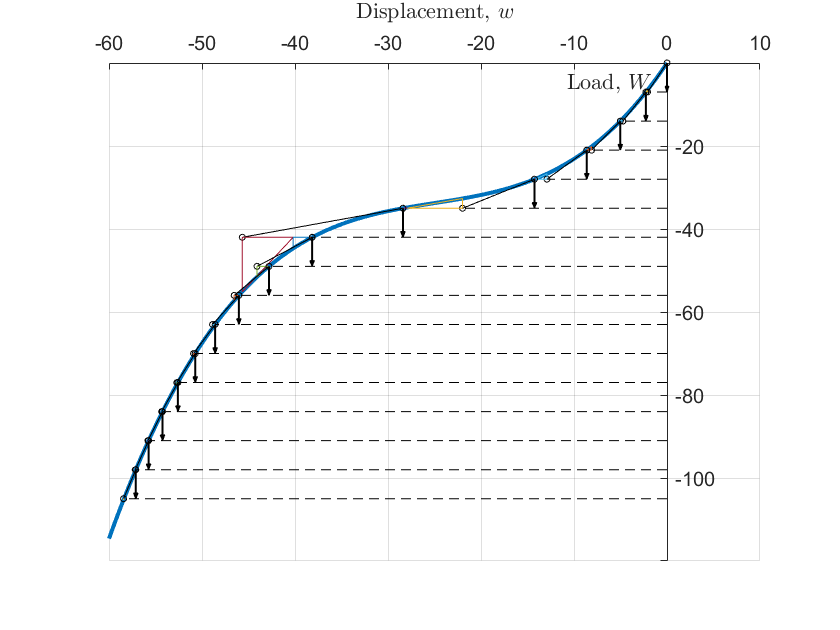
从上图可以看到，如果在非线性计算中

• 减小增量步的步长；
• 在每一个增量步进行迭代，使得残差小于某一个阈值

那么就能够得到相当不错的结果。